Musique et acoustique – Perspectives technico-scientifiques
Table des matières abrégée :
1. CORDES VIBRANTES ET TUYAUX SONORES
3. QUALITÉS PHYSIOLOGIQUES DES SONS MUSICAUX
Table des matières détaillée :
1. CORDES VIBRANTES ET TUYAUX SONORES
1. Ondes stationnaires le long d’une corde vibrante
2. FORMULE ET LOIS DES CORDES VIBRANTES
d. Formule des cordes vibrantes
3. ONDES STATIONNAIRES DANS LES TUYAUX
g. État vibratoire d’un tuyau « ouvert »
h. État vibratoire d’un tuyau « fermé »
4. FORMULES ET LOIS DES TUYAUX SONORES
i. Formules et lois des tuyaux ouverts
Vérification des lois précédentes
j. Formule et lois des tuyaux fermés
3. QUALITÉS PHYSIOLOGIQUES DES SONS MUSICAUX
Comparaison des intensités sonores
Influence de la distance de la source
r. Sons rendus par divers instruments
v. Gamme naturelle ou harmonique.
1. CORDES VIBRANTES ET TUYAUX SONORES
1. Ondes stationnaires le long d’une corde vibrante
a. Corde vibrante
On appelle corde vibrante un fil élastique, tendu entre deux points fixes, et susceptible d’émettre un son musical par ses vibrations. Une telle corde, que nous supposerons toujours cylindrique et homogène, peut vibrer longitudinalement si on l’excite à la manière de la tige d’un tube de Kundt, ou transversalement si on l’écarte de sa position d’équilibre : nous n’envisagerons que les vibrations transversales.
Ces cordes peuvent être en acier (piano) ou en boyau de mouton (violon) ; on peut les alourdir en les entourant en hélice d’un fil de cuivre ou d’argent : on obtient les cordes filées des notes graves du piano ou du sol du violon.
Remarque : Une corde vibrante est élastique dans le sens de sa longueur ; les lois que nous allons étudier la supposent également sans raideur : lorsqu’elle n’est pas tendue, elle conserve la forme qu’on lui donne.
b. Excitation de la corde
Pour écarter la corde de sa position d’équilibre, on peut la pincer avec le doigt (harpe), avec un onglet (mandoline, guitare), ou avec une plume ou épine, commandées par les touches d’un clavier (clavecin, épinette). La corde peut être frappée par un marteau garni de feutre (piano), ou même grattée par une roue (vielle). Enfin dans le violon et les instruments du même type, elle est attaquée par un archet, constitué par un grand nombre de crins tendus et enduits de colophane pour augmenter leur adhérence à la corde. L’archet, appuyé sur la corde, entraîne celle-ci par frottement en ABC (fig . 238), jusqu’au moment où l’élasticité de la corde l’emporte sur les forces de frottements et ramène celle-ci à sa position d’équilibre ABC ; le même phénomène se reproduit un grand nombre de fois par seconde, et il se trouve que sa période est celle de la vibration de la corde, par suite d’un phénomène de résonance mécanique.
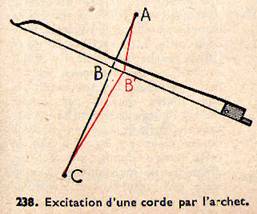
Fig.238 |
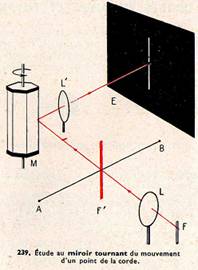
Fig.239 |
c. Mouvement de la corde
Nous avons déjà étudié l’état vibratoire d’une telle corde tendue entre deux points fixes. Nous savons qu’elle est le siège d’un système d’ondes stationnaires présentant un nœud de vibration à chaque extrémité (voir en particulier expérience de Melde, étude par stroboscopie).
Étudions plus en détail le mouvement d’un point de la corde. À l’aide d’une lentille L (fig. 239) faisons une image réelle F’ d’une fente lumineuse F juste sur une corde vibrante AB et perpendiculairement à celle-ci. La lumière tombe ensuite sur un miroir tournant M, et une lentille L’ donne sur un écran E une image nette de F’ en travers de laquelle on voit en noir la trace nette de la corde. Si on excite la corde en faisant tourner le miroir, il s’établit aussitôt le régime d’ondes stationnaires correspondant aux conditions aux limites définies par l’expérience ; l’image de la fente donne une bande blanche et la trace de la corde qui se meut de haut en bas de cette image donne une courbe, graphique du mouvement. On constate que celui-ci est sinusoïdal dans le cas d’une corde pincée (fig. 240), mais simplement périodique (et de même période que précédemment) dans le cas d’excitation par l’archet : le son dans ce dernier cas est beaucoup plus riche en harmoniques. Le son du violon a un timbre plus riche que celui de la harpe, qui donne un son clair et presque pur bien caractéristique de cet instrument.
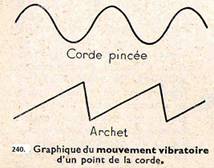
Fig.240 |
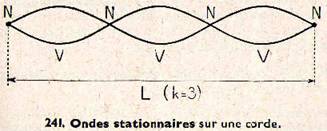
Fig.241 |
2. FORMULE ET LOIS DES CORDES VIBRANTES
d. Formule des cordes vibrantes
Nous savons qu’une corde fixée à ses deux extrémités présente toujours un nœud de vibration à ces extrémités, et un certain nombre d’autres nœuds intermédiaires ; le système d’ondes stationnaires se manifeste par un nombre entier de fuseaux répartis le long de la corde. S’il y a k fuseaux, la longueur de chacun d’eux (distance entre deux nœuds consécutifs) étant d’une demi-longueur d’onde, et si L est la longueur totale de la corde (fig. 241), on a :
L = kλ/2
et N étant la fréquence, et V la célérité des ondes transversales, λ = V/N
donc : L = kV/2N
Mais cette célérité a pour valeur
V = rac (F/μ) (rac = racine carrée)
où F est la tension en dynes de la corde, et μ la masse par unité de longueur. On en déduit
L = (k/2N) rac(F/μ) soit N = (k/2L) rac (F/μ)
Avec k = entier – L = longueur en mètres – F = tension en newtons – μ = masse par unité de longueur en kg/m.
Cette formule est valable dans tout autre système cohérent d’unités.
e. Lois des cordes vibrantes
Les lois résultent de la formule précédente.
La fréquence du son rendu par une corde vibrante (pour une valeur de k déterminée) est
inversement proportionnelle à la longueur de la corde (loi des longueurs) ;
proportionnelle à la racine carrée de la tension (loi des tensions) ;
inversement proportionnelle à la racine carrée de la masse par unité de longueur de corde (loi des masses).
Les divers sons partiels que peut rendre la corde correspondent aux divers systèmes d’ondes stationnaires susceptibles de s’établir, c’est-à-dire aux différentes valeurs de k. Si k = 1 (un seul fuseau), la corde donne le son fondamental. La formule montre que les sons partiels que peut rendre une corde sont tous les harmoniques du son fondamental (loi des harmoniques).
Remarque : La corde peut émettre séparément ou simultanément ses harmoniques, qui accompagnent presque toujours le son fondamental, surtout dans l’excitation par l’archet.
Vérifications expérimentales
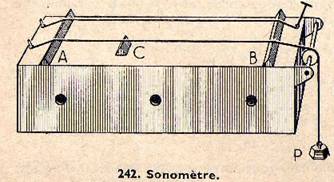 fig.242
fig.242
On emploie le sonomètre, constitué par une caisse de résonance (fig. 242) sur laquelle est tendue la corde à expérimenter dont on peut faire varier la tension au moyen de poids tenseurs ; cette corde est voisine d’une corde de comparaison réglable au moyen d’une clef. Nous supposerons que l’observateur sait apprécier l’unisson, qui correspond à l’égalité des fréquences. Les cordes étant d’abord à l’unisson, plaçons un chevalet mobile C, sous la corde AB, par exemple au tiers de sa longueur ; on observe que la partie AC rend un son plus aigu (fréquence plus élevée) que la partie CB, elle-même émettant un son plus aigu que la corde de comparaison. Les musiciens pourront reconnaître que la partie AC rend un son à l’octave aigu (fréquence double) du son rendu par CB.
Remarque : Une corde de violon a une tension constante ; le violoniste, en appuyant la corde sur la « touche » à des endroits déterminés, modifie la longueur vibrante ; les sons sont d’autant plus aigus que cette longueur est plus petite.
En faisant varier le poids tenseur P, on modifie la hauteur du son rendu par une corde donnée, et on peut ainsi vérifier que plus le poids tenseur est grand, plus la note rendue est aiguë. Pour élever le son d’un octave, il faut multiplier le poids tenseur par 4.
Remarque : Les cordes vocales de la voix humaine sont des membranes vibrantes qui se tendent plus ou moins sous l’action des muscles.
On a observé récemment que le courant d’air venant des poumons n’était pas nécessaire pour produire leur vibration, due, semble-t-il, à l’action du système nerveux.
On peut faire une vérification de la loi des masses en tendant sur le sonomètre deux cordes de même longueur, de même nature, tendues par le même poids, mais l’une ayant un diamètre plus grand que celui de l’autre. On observe que la corde la plus grosse rend une note plus grave que l’autre.
Remarque : Les cordes filées du piano ou du violon sont volontairement alourdies pour qu’on puisse obtenir une note grave avec une tension suffisante, tension indispensable pour ne pas entendre un bruit de « ficelle » et assurer une vibration régulière.
Les vérifications précédentes sont purement qualitatives. Mais, comme nous l’avons signalé, un expérimentateur musicien, qui saurait apprécier quelques intervalles musicaux tels que la tierce, la quarte, la quinte, l’octave, et qui connaîtrait la valeur des rapports de fréquences qui s’y rapportent vérifierait sans difficulté les lois du point de vue quantitatif.
Pour vérifier la loi des harmoniques d’une corde, touchons par exemple très légèrement cette corde en son milieu pendant qu’elle vibre ; nous supprimons le son fondamental auquel correspondait un ventre en cet endroit, mais la corde continue de vibrer en rendant l’octave de la note précédente. C’est ainsi que les violonistes, en effleurant la corde du violon en un en- droit convenable, font rendre à cette corde tel ou tel harmonique.
Disposons des petits cavaliers de papier sur une corde tendue comme l’indique la figure 243 ; excitons la corde entre C et B ; l’autre partie entre en vibration : les cavaliers sont chassés aux ventres mais restent en place aux nœuds.
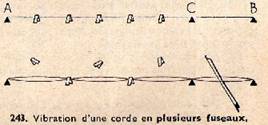 fig.243
fig.243
Remarque : Les marteaux du piano frappent les cordes au 1/7 ou 1/9 de leur longueur ; il ne peut alors se produire de nœud à cet endroit, et on évite ainsi la présence du 7ème ou du 9ème harmonique qui donneraient un timbre désagréable : il est facile de voir que ces harmoniques ne font pas partie de l’accord parfait du son fondamental.
3. ONDES STATIONNAIRES DANS LES TUYAUX
f. Tuyau sonore
On appelle tuyau sonore un tube de bois ou de métal en général cylindrique de section circulaire ou rectangulaire, à l’intérieur duquel l’air en vibration présente un système d’ondes stationnaires correspondant à une fréquence audible. Nous avons étudié ce phénomène vibratoire et nous savons qu’il est caractérisé par des ventres de vibration (nœuds de pression) équidistants d’une demi-longueur d’onde, entre lesquels s’intercalent exactement des nœuds de vibration (ventres de pression), lorsqu’il s’agit d’ondes planes, ce qui est le cas pour un tuyau cylindrique.
La source qui produit la vibration est à une extrémité du tuyau c’est une embouchure de flûte ou une anche, actionnée par un courant d’air. Cette source émet un son mal défini, très complexe, dépendant de la violence du courant d’air et dans lequel se trouve la fréquence convenable pour produire le système d’ondes stationnaires dans un tuyau donné (conditions aux limites).
Un tuyau sonore est un résonateur qui entre en résonance sur une des vibrations de la source.
Le tuyau vibrant réagit alors sur la source ; les vibrations autres que celle que renforce le tuyau sont très rapidement amorties.
g. État vibratoire d’un tuyau « ouvert »
Un tuyau est ouvert lorsqu’il communique avec l’atmosphère par son extrémité opposée à l’embouchure que nous supposerons en communication permanente avec l’atmosphère.
Les deux extrémités du tuyau, où règne une pression constante, sont des nœuds de pression, et par conséquent des ventres de vibration.
Dans un tuyau ouvert il y a toujours un ventre de vibration à chaque extrémité.
S’il n’y a que ces deux ventres le tuyau rend le son fondamental ; mais il peut y en avoir d’autres (fig. 244), correspondant aux divers sons partiels.

Fig.244 |
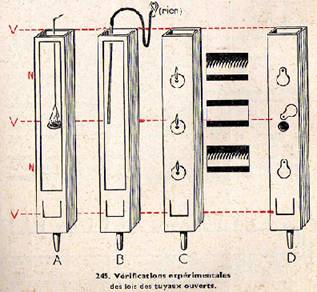
Fig.245 |
Expériences
Les expériences suivantes permettent de vérifier les résultats généraux connus relativement aux systèmes d’ondes stationnaires dans un tuyau ouvert. Descendons dans le tuyau une petite nacelle (fig. 245 A) dont le fond est une feuille de papier tendu, saupoudrée de sable ; si l’une des faces du tuyau est en verre, nous voyons le sable sautiller aux ventres de vibration. On peut enfoncer dans le tuyau (fig. 245. B) un tube de verre relié à l’oreille par un tube de caoutchouc ; lorsque la pression est constante à l’extrémité du tube de verre, l’oreille n’est pas affectée : on n’entend presque rien aux ventres de vibration. On trouve dans les cabinets de physique des tuyaux dont une paroi est munie de capsules manométriques (fig. 245C) : la flamme manométrique reste immobile aux nœuds de pression, donc aux ventres de vibration. Il existe également des tuyaux dont on peut démasquer certains trous percés dans la paroi (fig. 245 D) on oblige un nœud de pression, donc un ventre de vibration à s’établir en cet endroit ; si le système d’ondes stationnaires précédent est de ce fait modifié, la hauteur du son varie. On peut aussi régler des tuyaux à l’unisson, observer des battements en déplaçant une plaquette percée au voisinage de l’extrémité ouverte du tuyau.
h. État vibratoire d’un tuyau « fermé »
Un tuyau est fermé lorsque l’extrémité opposée à l’embouchure est munie d’un fond, jouant le rôle d’obstacle fixe indéformable dans l’établissement du système d’ondes stationnaires. Il se produit donc un nœud de vibration sur ce fond, mais un ventre subsiste à l’embouchure (nœud de pression).
Dans un tuyau fermé, il y a toujours un nœud de vibration à l’extrémité fermée, et un ventre de vibration à l’embouchure.
À cette disposition correspond le son fondamental (fig. 246) ; il peut s’intercaler entre le fond et l’embouchure d’autres nœuds et ventres correspondant aux divers sons partiels.

Fij.246 |

Fig.247 |
Expériences
Les dispositifs de la figure 245 A et 8 ne conviennent plus aux tuyaux fermés ; on peut par contre utiliser les dispositifs C et D. Citons la belle expérience de Rubens (1865-1922) : Un tuyau de poêle est percé de nombreux trous le long d’une génératrice (fig. 247). Fermé à une extrémité, il est mis en vibration à l’autre par une membrane élastique m devant laquelle on produit un son intense au moyen d’un diapason ou d’un tuyau sonore, convenablement choisis pour qu’il y ait résonance.
Un courant de gaz d’éclairage s’échappe par les trous ; les flammes obtenues paraissent d’autant plus longues que l’amplitude des variations de pression est plus considérable (ventres de pression ou nœuds de vibration).
4. FORMULES ET LOIS DES TUYAUX SONORES
i. Formules et lois des tuyaux ouverts
Reprenons la figure 244. Puisqu’il existe toujours un ventre à chaque extrémité d’un tuyau ouvert de longueur L (comptée à partir de l’embouchure), cette longueur est un multiple entier k d’intervalles VV, soit de la demi-longueur d’onde λ/2 : L = k λ/2
Si N est la fréquence du son émis et V la célérité du son dans le gaz qui emplit le tuyau : λ = V/N.
On en déduit N = kV/2L
K = 1 correspond au son fondamental, k = 2, 3, 4, etc., aux divers partiels. La formule montre que toutes les fréquences possibles sont tous les multiples entiers de la fréquence fondamentale, donc tous les harmoniques.
La formule trouvée permet d’énoncer les lois de Daniel Bernouilli.
Lois des tuyaux ouverts
1. La fréquence du son émis par un tuyau ouvert cylindrique (pour une valeur de k déterminée) est
indépendante de la substance et de la forme de sa section ;
inversement proportionnelle à la longueur du tuyau ;
proportionnelle à la célérité du son.
2. Les sons partiels sont constitués par tous les harmoniques du son fondamental.
EXEMPLE. — La célérité du son dans l’air étant de 340 m/s, calculer la longueur du tuyau qui émet un son fondamental de fréquence 435.
De la formule générale on tire L = kV/2N
Ici : k = 1, V =340 m/s, N = 435, donc : L = 340/ 2 x 435, soit L = 0,39 m.
Vérification des lois précédentes
On vérifie facilement que des tuyaux ouverts de même longueur, mais de section circulaire ou carrée, en bois, en carton, en métal, donnent la même note. Un tuyau plus long qu’un autre émet un son plus grave que le son émis par l’autre. On peut chauffer un tuyau par une résistance parcourue par un courant ; au fur et à mesure que la température s’élève, le son monte : en effet la célérité croît avec la température, et par conséquent la fréquence. Pour faire rendre à un tuyau ses sons partiels, on peut forcer le vent ; les harmoniques prennent successivement une intensité prépondérante et cela d’autant plus facilement que le tuyau est plus étroit.
Remarque : En réalité les ondes ne sont plus planes lorsqu’on s’approche de l’extrémité ouverte du tuyau. Le ventre à cet endroit est en dehors du tuyau, à une distance de l’extrémité ouverte égale à 2 fois la « profondeur » du tuyau (correction de Cavaillé-Coll), c’est-à-dire à 2 fois la distance du biseau à la face opposée.
Le diapason d’un tuyau est le rapport de sa profondeur à sa largeur. Plus le diapason est étroit, plus grand est le nombre d’harmoniques qui vibrent en même temps que le fondamental ; le son est d’autant plus gambé ; dans l’orgue on passe ainsi du timbre de la flûte à celui de la viole de gambe ; nous étudierons la signification physique du timbre à propos des qualités physiologiques du son.
j. Formule et lois des tuyaux fermés
Reprenons la figure 246 ; on voit que le fond du tuyau et l’embouchure sont nécessairement distants d’un nombre impair de quarts de longueur d’onde, soit, k étant un entier quelconque :
L = (2k + 1) λ /4
Comme λ = V/N, on en déduit : N = (2k + 1) V/4L
k= 0 correspond au son fondamental, k = 1, 2, 3, etc., aux divers partiels. La formule montre que toutes les fréquences possibles sont les multiples (2k ± 1), c’est-à-dire impairs de la fréquence fondamentale.
Lois des tuyaux fermés
1. La fréquence d’un son émis par un tuyau fermé cylindrique (pour une valeur de k déterminée) est
indépendante de la substance et de la forme de sa section ;
inversement proportionnelle à la longueur du tuyau ;
proportionnelle à la célérité du son.
2. Les sons partiels sont constitués par les harmoniques impairs du son fondamental.
Vérifications expérimentales
On peut reprendre les mêmes expériences que pour les tuyaux ouverts. En forçant le vent, on n’entendra cette fois que les harmoniques impairs. Un tuyau fermé donne un son moins riche, plus sourd qu’un tuyau ouvert ; c’est le tuyau du jeu de « bourdon » de l’orgue.
On remarquera qu’un tuyau fermé donne la même note qu’un tuyau ouvert de longueur double : le premier a pour longueur un quart de longueur d’onde (son fondamental), le second une demi-longueur d’onde, ce qui fait bien la même longueur d’onde pour les deux, donc la même fréquence. La figure 248 représente un tuyau ouvert que l’on peut fermer en son milieu par une cloison mobile : la note reste inchangée.
Les tuyaux fermés de l’orgue ont un fond constitué par un tampon mobile permettant l’accord.
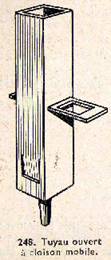
Fig.248 | 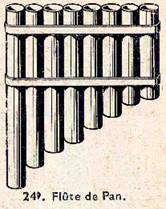
Fig.249 |
Remarque : On peut construire une flûte de Pan dont les longueurs des tubes (fig. 249) sont déterminées pour obtenir les notes successives de la gamme. On peut calculer qu’elles doivent être entre elles comme la suite des nombres : 180 – 160 – 160 – 144 – 135 – 120 – 108 – 96 – 90.
k. RÉSUMÉ
La fréquence du son rendu par une corde vibrante est donnée par
N = (k/2L) rac (F/ μ)
où k est l’ordre de l’harmonique, L la longueur de la corde en m, F sa tension en newtons, et μ sa masse par m de longueur. Cette formule est valable dans tout autre système cohérent d’unités.
Un tuyau ouvert à embouchure de flûte présente toujours un ventre de vibration à l’embouchure et un ventre à l’extrémité ouverte ; les sons partiels, relatifs à l’établissement d’autres ventres intermédiaires, sont les harmoniques du son fondamental ; la fréquence du son émis est
N = kV/2L (tuyau ouvert).
Un tuyau fermé à embouchure de flûte présente toujours un ventre de vibration à l’embouchure et un nœud à l’extrémité fermée ; les sons partiels, relatifs à l’établissement d’autres nœuds et ventres intermédiaires, sont les harmoniques Impairs du son fondamental ; la fréquence est donnée par
N = (2k+1)V/4L (tuyau fermé).
Les lois précédentes trouvent leurs applications pratiques dons les instruments de musique à cordes ou à vent.
2. LES INSTRUMENTS DE MUSIQUE
Les différents sons utilisés en musique ont des fréquences bien déterminées ; les notes se désignent par les noms bien connus de la gamme, affectés d’un indice qui sert à repérer la gamme elle-même parmi la succession de toutes les gammes. Lorsqu’un chef de chœur ou un chef d’orchestre écoute son diapason, il entend une note de fréquence 435, qui est la note la3. Le musicien caractérise donc une note par un nom, tandis que le physicien la caractérise par sa fréquence. Dans cette lecture qui intéressera surtout les musiciens, nous appellerons les notes par leurs noms.
5. Les instruments à cordes.
Le piano comporte 85 notes (le clavecin n’en avait que 45) du la-2, au la6 ; les dix notes les plus graves sont données chacune par une corde filée, les douze suivantes par deux cordes filées frappées ensemble, puis les marteaux attaquent trois cordes par note, réglées à l’unisson. Cela fait 223 cordes, dont la tension moyenne de 40 kgp donne un effort total de 9 tonnes-poids environ.
Les cordes de la harpe sont pincées avec les doigts ; une pédale permet de bémoliser toutes les notes, par un raccourcissement convenable de la longueur vibrante.
 fig. 250
fig. 250
Les instruments du quatuor, c’est-à-dire le violon (fig. 250), l’alto, le violoncelle, la contrebasse, comportent 4 cordes passant dans les encoches d’un chevalet courbe (afin que l’archet puisse attaquer une corde sans toucher aux autres) ; le chevalet communique les vibrations à une caisse de résonance ; les cordes sont tendues par des chevilles sur lesquelles elles s’enroulent. La corde la plus grave du violon (sol2) est une corde filée ; les trois autres sont en boyau, sauf parfois la chanterelle (mi4) qui peut être en acier ; les tensions varient entre 5 et 10 kgp.
Les notes données par les cordes à vide sont les suivantes :
Violon : sol2, ré3, la3, mi4 (par quintes)
Alto : do2, sol2, ré3, la3 (par quintes)
Violoncelle : do1, sol1, ré2, la2 (par quintes)
Contrebasse : mi-1, la-1, ré1, sol1 (par quartes)
6. Les embouchures
Comme le nom l’indique, les embouchures sont les parties de l’instrument qui se placent à la bouche du musicien, et par extension à la source d’air qui actionne un instrument à vent quelconque. Elles sont de deux types : l’embouchure de flûte et l’embouchure à anche.
Pour jouer de la flûte on souffle de l’air rasant une ouverture pratiquée vers une extrémité du tube (fig. 251) ; il se produit des tourbillons saccadés, qui feront vibrer l’air du tube.
Le mécanisme est le même dans le tuyau d’orgue dit « à embouchure de flûte ». L’air d’un sommier, alimenté par une soufflerie, est guidé sur un biseau B de bois ou de métal qui produit les tourbillons ; l’air s’échappe par une lumière L. Il n’y a pratiquement pas de courant d’air dans le tuyau, qui peut être ouvert ou fermé à l’autre extrémité.
D’autre part, la pression à l’embouchure est égale à la pression atmosphérique, constante ; il y a donc un nœud de pression, donc un ventre du vibration.
Dans le cours qui précède, nous n’avons envisagé que des tuyaux du type à embouchure de flûte. Les lois relatives aux tuyaux actionnés par une embouchure à anche sont en effet un peu moins simples. Une anche est une lamelle de laiton (orgue) ou de roseau (clarinette) qu’un courant d’air fait vibrer. L’anche libre obstrue incomplètement une lumière, et peut vibrer de part et d’autre de celle-ci (fig. 252) ; le son rendu par le tuyau est alors riche en harmoniques ; son timbre rappelle celui de l’harmonium ou de l’accordéon, L’anche battante est un peu plus grande que la lumière, qui se trouve fermée périodiquement (fig. 253) ; le son est encore plus riche en harmoniques que dans le cas précédent (clarinette ; « bombarde » de l’orgue).
La longueur d’anche vibrante est réglée au moyen d’un rasette r, afin d’accorder la résonance entre la vibration de l’anche et celle de l’air du tuyau.
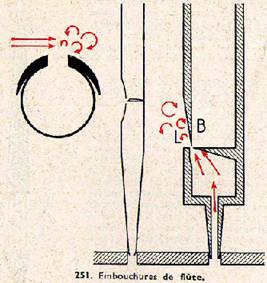
Fig.251 |
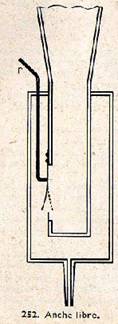
Fig.252 |
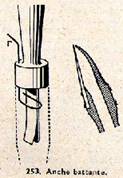
Fig.253 |
Pour entretenir le mouvement de l’anche, il faut un courant d’air dans le tuyau, qui ne peut donc être fermé à l’autre extrémité (ou alors seulement en partie) : on obtient des sons bouchés.
Signalons que le hautbois et le basson comportent une anche double, c’est-à-dire deux anches battant l’une contre l’autre.
Le tuyau sonore à embouchure à anche est presque toujours conique (orgue, clarinette) ; un tel tuyau comporte encore un système de ventres équidistants, de nœuds équidistants, mais l’ensemble des nœuds est déporté du côté de l’anche ; un nœud n’est plus au milieu de deux ventres.
De toute façon, l’anche joue le rôle d’un obstacle indéformable ; il y a un nœud de vibration au voisinage de l’anche.
Dans le cor, ou le clairon, ce sont les lèvres crispées de l’instrumentiste qui font office d’anche.
7. Les instruments à vent
L’orgue utilise des séries de tuyaux différents, à embouchure de flûte (jeux de fond) ou à anches (jeux d’anches). Les tuyaux sont en bois (jeu de bourdon pour les tuyaux fermés, de flûte pour les tuyaux ouverts) ou en alliage métallique contenant de l’étain et parfois de l’argent (jeu de montre dont on voit les plus gros tuyaux sur la façade de l’orgue). À l’intérieur du buffet se trouvent de nombreux autres tuyaux (plusieurs milliers) cylindriques ou coniques, chaque jeu ayant un timbre bien caractérisé (salicional, viole de gambe, basson, etc.). Une touche de clavier fera parler autant de tuyaux correspondant à cette touche qu’on aura tiré de registres commandant chaque jeu. Certains jeux donnent même la tierce, la quinte, l’octave, la septième (jeux de mutation) de la note normale : on peut réaliser ainsi un ensemble sonore extrêmement varié. Les jeux sont répartis sur plusieurs claviers manuels et un pédalier. Outre les registres, se trouvent des dispositifs d’expression et de combinaisons des claviers et du pédalier les uns avec les autres. La figure 254 représente une console d’orgue. Tous les sons audibles sont utilisés, depuis le do-2 au do7 ; une soufflerie à faible pression doit débiter parfois jusqu’à plusieurs mètres cubes d’air par seconde.

Dans le trombone à coulisse les différentes notes sont données en faisant varier la longueur du tuyau au moyen d’une coulisse ; dans le cornet à pistons, on modifie la longueur du tuyau en appuyant sur des touches qui introduisent ou suppriment des portions supplémentaires de tubs.
Dans la flûte, la clarinette ou le saxophone (anche battante en roseau), le hautbois ou le cor anglais (anche battante double), le tuyau a une longueur fixe, mais on débouche des trous, soit directement avec les doigts, soit au moyen de clefs, ce qui provoque l’émission des sons partiels convenablement choisis.
Le clairon, le cor et les instruments analogues n’émettent qu’un nombre limité de notes, harmoniques d’un son fondamental obtenus en forçant plus ou moins le vent ; le clairon donne certains harmoniques de do1, soit : sol2, do3, mi3, sol3.
3. QUALITÉS PHYSIOLOGIQUES DES SONS MUSICAUX
8. INTENSITÉ
l. Sons musicaux
Les sons perçus par l’oreille peuvent se classer en bruits et en sons musicaux. Le son produit par un coup de fusil ou une explosion est un bruit ; un sifflet, un violon, un piano émettent des sons musicaux. Les bruits sont toujours produits par des trains d’ondes nettement séparés, et de constitution complexe ; les sons musicaux résultent de vibrations plus simples, et sont caractérisés par trois qualités physiologiques : l’intensité, la hauteur et le timbre.
Sons intenses ; sons faibles
Un instrument de musique peut jouer fort ou doucement : nous dirons que dans le premier cas les sons émis sont plus intenses que dans le second. Il est facile de constater que le son est d’autant plus intense que la source, pour une fréquence donnée, vibre avec une plus grande amplitude : le violon émet un son intense quand l’archet attaque fortement la corde ; le piano émet une note intense quand la touche est enfoncée énergiquement. Il est d’ailleurs assez évident que l’oreille sera d’autant plus fortement affectée que le son lui apportera une plus grande énergie vibratoire nous savons que celle-ci croît comme le carré de l’amplitude.
L’intensité d’un son dépend de l’amplitude de la vibration sonore.
Seuil d’audibilité
Si l’oreille ne capte pas une énergie vibratoire suffisante, on n’entend rien ; un murmure trop faible ne se perçoit pas. On ne commencera à « comprendre » un son qu’a partir d’une certaine intensité correspondant au seuil d’audibilité. Par contre, si le son devient trop intense, on dit communément qu’ « il déchire les oreilles » : il a atteint le seuil de douleur ; son audition n’est plus supportable (sifflet de locomotive lorsqu’on est très près).
D’autre part, le tympan est sensible aux variations de pression. Nous avons calculé la valeur de l’amplitude ΔP de la variation de pression, et montré qu’elle était proportionnelle à l’amplitude de la vibration. Pour simplifier, on appelle pression acoustique cette amplitude p de la variation de pression ; elle est de l’ordre de 2x10-4 baryes pour l’audition habituelle.
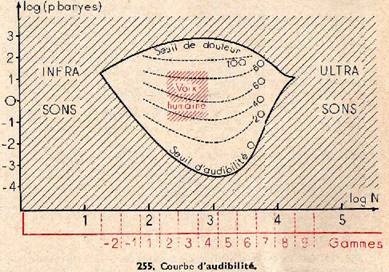 Fig.255
Fig.255
Le graphique de la figure 255 montre comment les seuils d’audibilité et de douleur dépendent à la fois de la fréquence N et de la pression acoustique p. On obtient un domaine fermé d’audibilité, limité à la fois en fréquence par les infra-sons et les ultra-sons, et en intensité par les seuils. À chaque fréquence correspond ainsi un seuil d’audibilité et un seuil de douleur qui se rejoignent aux limites des fréquences audibles.
Pour les élèves musiciens, l’axe des abscisses, chiffré en logarithmes de la fréquence, a été doublé par l’indication des numéros des gammes où se situent les sons envisagés.
Comparaison des intensités sonores
Il est naturel de définir physiquement l’intensité d’un son comme proportionnelle à l’énergie vibratoire captée par l’oreille ; or celle-ci est proportionnelle au carré de l’amplitude et par conséquent au carré de la pression acoustique p. Nous poserons
I =kp2
La loi de Fechner exprime que les sensations croissent comme les logarithmes des excitations. La différence des sensations produites par deux sons d’intensités I1 et I2 pourra donc être mesurée par
log I2 — log I1 = 2 (log p2 — log p1)
log I2 — log I1 est exprimé en bel (bl). On emploie surtout le décibel (dbl ; dixième partie du bel). Il se trouve que le décibel correspond à peu près à la plus petite différence d’intensité appréciable par l’oreille.
Très souvent, l’intensité de référence I, est celle qui correspond, pour une fréquence donnée, au seuil d’audibilité auquel on attribue un niveau physique d’intensité égal à zéro. Le nombre de décibels trouvé mesurera le niveau physique d’intensité du son donné.
EXEMPLE. — Pour une fréquence voisine de 500, le seuil d’audibilité correspond à une pression acoustique de 0,001 barye et le seuil de douleur à une pression acoustique de 320 baryes. Calculer combien de décibels séparent les intensités sonores correspondantes,
En bels, la différence cherchée vaut
2(log p2 — log p1) = 2 log(p2/p1)
et en décibels : 20 log(p2/p1) = 20 1og320000
Soit 20 x 5,50515 -= 110,1 décibels.
Ce nombre mesure également le niveau physique du seuil de douleur.
Remarque :Nous venons de chiffrer les niveaux physiques d’intensité d’un son de fréquence donnée. Mais il est difficile d’apprécier à l’oreille lequel est le plus intense d’un certain son grave ou d’un certain son aigu. Mais en appréciant des égalités d’intensités sonores pour des fréquences très voisines, on a pu déterminer des courbes isophones : le long de chacune d’elles (représentées en pointillé sur la fig. 255) ; le niveau physiologique d’intensité est le même. Il est mesuré en phones, les phones coïncidant avec les nombres de décibels du niveau physique pour la fréquence 1000.
Influence de la distance de la source
L’expérience journalière montre que l’intensité d’un son décroît quand on s’éloigne de la source. Nous savons que les vibrations s’amortissent par suite des frottements. Mais une autre raison intervient. L’énergie vibratoire E émise par une source O (fig. 256) à un instant donné est répartie sur une surface d’onde Σ, sphère de rayon d centrée sur O. À cette distance d de la source, l’oreille capte, par sa surface utile s, l’énergie
e = E (s/Σ)
tandis qu’a la distance d’, elle capterait
e’ = E (s/Σ’)
On voit que :e’/e = Σ/Σ’ / d²/d’²
et de ce fait l’intensité varie en raison inverse du carré de la distance.
Par contre, un cornet acoustique capterait, par la surface de son pavillon S > s, une énergie vibratoire plus grande que l’oreille seule ; le seuil d’audibilité du système (oreille + cornet) est plus bas que celui de l’oreille seule ; d’où l’utilisation du cornet par les personnes dures d’oreille.
 Fig 257
Fig 257
Le porte-voix (fig. 257) oblige l’énergie vibratoire à rester à l’intérieur d’un cône ayant pour sommet la source (il y a cependant une diffraction appréciable) au lieu de la laisser se répartir sur des surfaces d’ondes sphériques. La portée de la voix s’en trouve accrue (distance maximum de la source à l’observateur qui doit comprendre ce qu’on lui dit).
9. HAUTEUR
m. Sons graves ; sons aigus
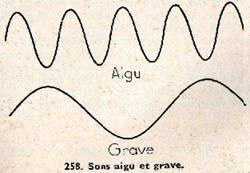 Fig.258
Fig.258
Nous avons naturellement la notion d’un son plus aigu ou plus grave qu’un autre : les cordes d’un violoncelle donnent des sons plus graves que celles d’un violon. Les notes d’un piano correspondant à la droite du clavier sont plus aiguës que celles de gauche. On dit aussi que les notes graves sont basses, que les notes aiguës sont hautes : l’acuité d’un son n’est autre que sa hauteur.
Or dans l’expérience de la lame de scie, nous avons constaté que le son devenait de plus en plus aigu au fur et à mesure que croissait la fréquence ; l’enregistrement graphique de deux diapasons montre qu’au son le plus grave correspond la fréquence la plus petite (fig. 258) ; lorsqu’un moteur se met en marche, on entend un son qui devient de plus en plus aigu : c’est le son d’axe dont la fréquence augmente (une ou deux impulsions par tour) en même temps que la vitesse de rotation du moteur.
Nous voyons que la sensation physiologique de hauteur est liée à la valeur physique de la fréquence.
Définition. L’acuité d’un son augmentant avec la fréquence, nous mesurons la hauteur d’un son par la valeur de sa fréquence.
n. Les sirènes
|
|
|
|
Le nom de ces appareils vient de ce que primitivement ils devaient fonctionner dans l’eau (les liquides transmettent les vibrations sonores, voir § 238) : il n’est pas interdit à un scientifique de se souvenir de la mythologie.
La sirène simple, ou de Seebeck, consiste en un simple disque percé de p trous équidistants, répartis sur une même circonférence (fig. 259) ; un dispositif mécanique lui communique une rotation de n tours par seconde. Un ajutage A envoie un jet d’air comprimé au niveau des trous, qui laissent évidemment passer l’air n x p fois par seconde. À ces impulsions correspondent des vibrations sonores, assez compliquées, mais dont la fréquence principale, ou fondamentale, est N = n x p.
La sirène de Cagniard de la Tour (physicien français, 1777-1859) émet les vibrations sonores d’après le même principe, mais le courant d’air entretient le mouvement de l’appareil qui est une véritable petite turbine. L’air arrive (fig. 260) par p ajutages inclinés disposés régulièrement le long d’une circonférence d’un plateau fixe A. Le plateau tournant B de la sirène, tout contre le précédent, comporte p ouvertures analogues, disposées de la même façon, mais inclinées en sens contraire. Les jets d’air, agissant sur les parois de ces trous, provoquent la rotation du plateau.
On notera que les ouvertures se trouvent toutes démasquées ou toutes obstruées en même temps, et avec p jets d’air le son sera plus fort qu’avec un seul dans la sirène de Seebeck. Si le plateau fait n tours par seconde, les ouvertures seront démasquées toutes ensemble n fois par seconde, et la fréquence vaudra encore ici : N = n x p.
La valeur de n peut être mesurée à l’aide du compte-tours C que porte l’appareil.
EXEMPLE. — Le plateau d’une sirène porte 25 trous et fait 174 tours en 10 secondes, quelle est la hauteur du son perçu ?
Il y a par tour 25 jets d’air, et en 10 secondes il y a eu 174 x 25 = 4 350 impulsions.
La fréquence cherchée est N = 4350/10, soit N =435.
On observe très bien, qualitativement, que le son « monte » quand la vitesse de rotation de la sirène croît.
Les sirènes sont utilisées comme signaux avertisseurs sirènes d’usines, sirènes de brume sur les côtes, sirènes d’alerte, on modifie la hauteur du son émis précisément en faisant varier la vitesse de rotation, quelquefois automatiquement.
o. Mesure d’une fréquence
En principe, une fréquence musicale peut être mesurée à l’aide d’une sirène ; il suffira d’amener celle-ci à l’unisson du son étudié : deux sons musicaux sont à l’unisson lorsqu’ils donnent la même sensation de hauteur. La fréquence cherchée est alors celle du son de la sirène, mesurable à l’aide du compte-tours de l’instrument et d’un chronomètre.
Le réglage à l’unisson est extrêmement sensible ; si les fréquences n’étaient pas rigoureusement égales, par exemple 500 et 501, nous savons qu’on percevrait des battements, a raison de 1 par seconde : la précision serait déjà de 1/500. On règle presque exactement l’unisson en faisant disparaître les battements.
p. Fréquences audibles
Nous avons déjà vu que les sons audibles avaient des fréquences comprises entre 20 et 20 000. Ces limites ne sont pas strictes, et dépendent de l’observateur ainsi que des conditions de l’expérience. Quand une sirène se met en mouvement, on se rend bien compte que la sensation sonore n’apparaît que pour une vitesse de rotation suffisante, facile à mesurer ; on dit que le seuil d’audibilité est atteint. La dernière touche à gauche du piano, qui est un la, donne un son de 27 vibrations par seconde. Le tuyau d’orgue de 32 pieds (plus de 10 m), donne une note correspondant à 16 vibrations par seconde ; lorsqu’il parle seul, on ne sait pas trop si l’on entend un ronflement ou un son musical : l’oreille est égarée. Au-dessous de cette fréquence se situent les infra-sons.
La limite supérieure, pour les sons tellement aigus que l’on n’entend plus la note, se situe entre 17 000 et 20 000. Ne pas croire que cet écart est grand : le passage d’une fréquence à l’autre ne correspond qu’a l’intervalle de sixte environ. Au-dessus de cette fréquence se situent les ultra-sons. Les sons proprement musicaux n’ont pas une fréquence supérieure à 5000.
Beaucoup d’animaux sont sensibles aux ultrasons ; on sait que les chauves-souris évitent la nuit les obstacles en émettant des ultra-sons que réfléchissent ces obstacles et dont elles perçoivent l’écho. Les chiens peuvent répondre à l’appel d’un sifflet à ultra-son l’oreille humaine n’entend rien.
On produit maintenant des ultra-sons par des sirènes, mais le procédé le plus courant consiste à faire osciller une lame de quartz piézo-électrique. Si, à l’aide d’un condensateur alimenté en courant alternatif, on charge et décharge un grand nombre de fois par seconde les faces de la lame, celle-ci se met à vibrer (phénomène de piézo-électricité.) Elle présente un système d’ondes stationnaires ;
si l’épaisseur est e = 0,5 mm, V = 5 000 m/s la célérité du son dans le quartz ;
e = λ/2 = V/2N, d’où : N = V/2e = 5000000.
Les échos d’ultra-sons servent au repérage sous-marin (bateaux, rochers, bancs de poissons) ; ces vibrations transportent une grande énergie : E = 2a²(pi)²mN², à cause de la grande valeur de N : on les utilise dans certaines machines à laver le linge, pour homogénéiser les émulsions, étudier l’homogénéité des pièces métalliques, etc.
La portée d’utilisation des ultrasons est beaucoup plus forte dans l’eau que dans l’air, et beaucoup plus forte que les fréquences sont plus basses.
Les ultra-sons ont reçu des applications en médecine.
q. Intervalles musicaux
Reprenons une sirène de Seebeck dont le plateau comporte deux séries de trous, par exemple 8 et 12 (fig. 264) ; pour une vitesse de rotation donnée du plateau, le passage des 12 trous donnera un son plus aigu que le passage des 8. En disposant de deux ajustages amenant l’air comprimé, on pourra entendre les deux sons simultanément : ce sera un accord. Or un musicien reconnaît dans cet accord un intervalle de quinte, le même que donneraient deux cordes consécutives d’un violon, à vide. Augmentons la vitesse de rotation du disque les deux sons s’élèvent, mais l’intervalle de quinte subsiste. Or, chaque fréquence ayant varié, leur rapport est resté constant et égal à 12/8 = 1,5.
Un intervalle musical de nature donnée ne dépend que du rapport des fréquences des sons qui le constituent ; nous mesurerons cet intervalle par ce rapport des fréquences
I = N2/N1
Tous les intervalles musicaux ne sont pas agréables à l’oreille ; lorsque la fraction N2/N1 est très simple, l’accord dorme une impression de platitude ; quand N2/N1 devient de moins en moins simple, l’impression musicale est de plus en plus riche, jusqu’à devenir désagréable ; on passe ainsi des intervalles consonants aux intervalles dissonants.
Par exemple
intervalles consonants : unisson : I = 1 — octave : I = 2 — quinte : I = 3/2
intervalles dissonants : seconde : I = 9/8 — septième : I = 15/8
Considérons trois sons de fréquences croissantes N1, N2, N3. L’intervalle total des sons extrêmes I = N3/N1 est formé de la suite des deux intervalles partiels I’ = N2/N1 et I" = N3/N2
Or on a évidemment N3/N1 = N3/N2 x N2/N1
Soit : I = I’ x I".
L’intervalle total est égal au produit des intervalles successifs qui le composent.
La formule I = I’ x I" s’écrit, en prenant les logarithmes
logI = log I’ + log I".
Cette relation conduit à une nouvelle façon de mesurer un intervalle par le moyen de son logarithme, ou mieux par mille fois son logarithme, afin d’éviter les décimales. Le nombre ainsi obtenu mesure l’intervalle donné en savarts (en abrégé : σ), nom d’un physicien français, Félix Savart (1791-1841).
Définition. Le nombre de savarts mesurant un intervalle donné est égal à 1000 fois le logarithme de cet intervalle.
D’autre part comme
1000 log I = 1000 log I’ + 1000 log I",
on voit que
La mesure en savarts d’un intervalle total est égal à la somme des mesures en savarts des intervalles successifs qui le composent.
Une oreille exceptionnelle peut juste arriver à distinguer une différence de hauteur correspondant à un savart (1 σ) : cette unité est donc convenablement choisie. Une oreille courante distingue deux sons dont l’intervalle est de un comma.
Un comma = 81/80
Exprimons en savarts l’intervalle de comma. Nous calculerons 1000 log I =
1000 log I = 1000 (log 81 — log 80) = 1 000 (1,90849 — 1,90309) = 5,4 σ
10. TIMBRE
r. Sons rendus par divers instruments
Écoutons un violon et une clarinette émettre la même note avec une intensité analogue. Nous distinguons cependant chacun des instruments : nous dirons que le timbre de leur son n’est pas le même. En effet, chacune des vibrations n’est pas sinusoïdale : elle est simplement périodique ; sa fréquence correspond à la hauteur du son émis ; nous avons un son complexe. Une vibration sinusoïdale donnerait un son simple ; il n’en existe pas.
Le timbre d’un son est la qualité physiologique qui permet de distinguer deux sons de même hauteur et de même intensité, émis par des instruments différents.
s. Harmoniques
Nous savons qu’une vibration périodique quelconque peut être considérée comme la somme d’une vibration fondamentale de fréquence N et de ses harmoniques de fréquences 2N, 3N,… kN, … etc., où kN est la fréquence du k-ième harmonique (théorème de Fourier). Pour étudier un son complexe, c’est-à-dire provenant d’une vibration sonore périodique quelconque, il suffira ce rechercher comment cette vibration peut être décomposée en harmoniques.
Les différents timbres sont dus à la présence des harmoniques du son fondamental, qui entrent dans la composition du son résultant avec des intensités différentes selon les cas.
Un instrument tel que le hautbois ou la clarinette émet un son «étoffé», riche en harmoniques ; par contre la flûte ou le tuyau d’orgue d’un jeu de « bourdon » donne un son plus clair ou plus plat, pauvre en harmoniques.
Remarque : Un système vibratoire peut vibrer de diverses façons, chacune donnant, en sus du son fondamental, des sons dits partiels. Par exemple un diapason dont le son fondamental a pour fréquence 261 (ut3) a pour premier partiel une vibration de fréquence 827 (sol dièze), qui n’est pas un harmonique du son fondamental. Il ne faut pas confondre partiels et harmoniques. Si l’on excite un diapason, on entend d’abord un son complexe très désagréable, dû aux partiels ; ceux-ci s’éteignent rapidement, et il ne subsiste que le son fondamental à peu près pur (sinusoïdal) du diapason.
t. Analyse d’un son complexe
Certaines oreilles sensibles peuvent reconnaître la présence d’harmoniques dans un son complexe.
On peut maintenant recevoir le son sur un microphone ; un montage électrique assez compliqué permet de filtrer les harmoniques, de déceler leur présence et de mesurer leur intensité. La figure 265 représente l’analyse du timbre du basson, instrument de musique au son très timbré, jusqu’au 10ème harmonique ; on voit que tous les harmoniques sont présents avec une intensité appréciable, comparable à celle de la vibration fondamentale (et même parfois supérieure). Cette figure étant assez compliquée, on représente le résultat de l’analyse par le spectre acoustique ; le son complexe du basson est ainsi schématisé par la figure 266 : on porte en abscisses le numéro des harmoniques, et en ordonnées les intensités de chacun d’eux (proportionnelles aux carrés des amplitudes) ; on obtient ainsi une série de segments parallèles, raies acoustiques, l’ensemble rappelant les raies spectrales d’un spectre optique.
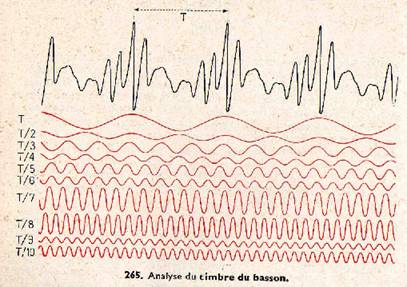 Fig. 265
Fig. 265
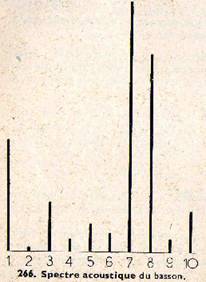 Fig. 266
Fig. 266
u. Synthèse d’un son complexe
Après avoir analysé les sons, Helmholtz imagina de les reconstituer à l’aide d une série de diapasons montés sur caoutchouc (pour éviter des couplages) et vibrant devant des résonateurs ; on pouvait modifier l’ouverture de ces derniers afin de régler l’intensité du son composant. Après maint tâtonnement, il fit la synthèse des sons du cor, du hautbois, de la voix humaine.
Devant un piano ouvert, chantons une voyelle (sur une note juste du piano), après avoir levé les étouffoirs. Certaines cordes entrent en vibration par résonance sur les harmoniques correspondants ; on reconnaît la voyelle d’après la résonance du piano, qui a réalisé sa synthèse.
L’orgue possède des jeux de tuyaux donnant tel ou tel harmonique de la note correspondant habituellement à la touche du clavier ; on peut combiner des timbres sonores, ce qui fait en grande partie la richesse de cet instrument.
Enfin, on a pu analyser les sons complexes en étudiant la bande sonore des films musicaux. On a réussi à faire entendre des sons « artificiels » et des mots que jamais personne n’a prononcés.
Les ensembles sonores de l’orchestre proviennent de l’emploi judicieux de tels ou tels groupes d’instruments, apportant chacun leur timbre propre ; les effets de fondu ou de contraste qui en résultent relèvent de la science de l’« orchestration ».
11. RÉSUMÉ
L’intensité d’un son dépend de son amplitude ; l’oreille est sensible à la pression acoustique. La sensation sonore ne se produit qu’à l’intérieur d’un domaine limité par les ultra-sons, les infra-sons, le seuil d’audibilité, le seuil de douleur.
Un son musical est d’autant plus haut qu’il est plus aigu, d’autant plus bas qu’il est plus grave : sa hauteur croît avec la fréquence, et se mesure par la valeur de cette fréquence. On peut avoir la valeur de la fréquence en réglant à l’unisson une sirène sur le son donné.
Le timbre d’un son est dû à la présence des harmoniques du son fondamental, qui interviennent chacun avec des intensités différentes. On peut analyser un son complexe en recherchant les harmoniques à l’aide de spectroscopes, et reconstituer un son de timbre donné.
4. LES NOTES MUSICALES
On n’utilise pas en musique des sons de hauteurs quelconques, mais des notes de fréquences bien déterminées. Lorsqu’on émet la succession de ces notes par hauteurs croissantes, la même mélodie se reproduit à chaque intervalle d’octave. À l’intérieur d’un intervalle d’octave, la succession des notes s’appelle la gamme.
Les notes ont reçu un nom propre, qui se répète à chaque intervalle d’octave.
... la si ut ré mi fa sol la si ut ré ...
Les noms des notes, employés en France, ont été proposés par Gui, moine de l’Abbaye de Pomposa, né à Arezzo en Toscane vers la fin du XVII siècle ; ce sont les premières syllabes des demi-vers d’un hymne à saint Jean Baptiste, que l’on chante précisément sur les notes correspondantes de la gamme
Ut queant laxis resonare fibris
Mira gestorum famuli tuorum
Solve polluti labii reatum
Sancti Johannes.
Le mot si (initiales de saint Jean) est attribué au compositeur français Le Maire. On remplace ut par do, en musique, syllabe plus facile à chanter.
En Allemagne et en Angleterre les notes de la gamme sont désignées par des lettres :
C, D, E, F, G, A, B.
La gamme diatonique signalée plus loin est du mode majeur ; il existe des gammes de modes mineur, dorien, etc. Les Grecs, les Arabes ont utilisé autrefois des gammes très particulières.
Chaque gamme est affectée d’un numéro d’ordre ; ce numéro augmente d’une unité à chaque ut rencontré en montant ; en France, le zéro n’est pas utilisé
- 2 ; - 1 ; 1 ; 2 ; 3 ; 4 ; etc.
On dira par exemple : ut-1 ; la4 ; ré5.
Pour définir la fréquence de toutes les notes, il suffit maintenant de fixer la fréquence de l’une d’elles. Depuis 1859, on adopte en France : la3 = 435.
Il fut nécessaire de fixer la fréquence du la3 qui ne cessait d’augmenter ; de 405 sous Louis XIV, elle passait à 423 sous l’Empire ; on la fixa à 435 pour donner plus d’éclat aux cuivres. Les Anglais utilisent 457, et les Allemands 440 pour l’orchestre.
On envisage parfois une échelle « des physiciens » définie par ut-2 = 16 ; elle conduit à la3 = 430,54 mais toutes les fréquences des ut sont de puissances de 2.
v. Gamme naturelle ou harmonique.
Cette gamme fut préconisée au début du XVIe siècle par Zarlino, prêtre et musicien italien. Les 7 notes habituelles sont telles que leurs harmoniques sont en général d’autres notes de cette gamme, d’où son nom. Mais c’est aussi la gamme qu’un bon chanteur (ou un bon violoniste) utilise naturellement, ainsi que Helmholtz et Rameau l’ont montré, puisque, si l’on émet deux notes successivement, la deuxième note avait déjà été entendue dans les harmoniques de la précédente. Comme ce n’est pas le cas de la gamme tempérée, celle-ci est fausse du point de vue musical, et fut considérée comme une monstruosité au XVIIIe siècle : mais elle est seule utilisable sur les instruments à sons fixes, sinon il faudrait multiplier les touches du clavier comprises dans l’octave.
Les intervalles des notes de la gamme naturelle sont ainsi définis par rapport à la tonique ut
| ut | ré | mi | fa | sol | la | si | ut |
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
Cherchons les harmoniques de ut1 de fréquence N.
Premier harmonique : N1 = ut1
Deuxième harmonique : N2 = 2N1 = ut2
Troisième harmonique : N3 = 3N1 = 3/2N2 = sol2
Quatrième harmonique : N4 = 4N1 = 4N2 = ut3
Cinquième harmonique : N5 = 5N1 = 5/2N4 = mi3
Sixième harmonique : N3 = 6N1 = 3/2N4 = sol3
Tous ces harmoniques forment un accord parfait ; mais le 7ème et le 11ème ne figurent pas dans la gamme ; ce sont d’ailleurs des harmoniques éloignés.
On peut calculer facilement les intervalles successifs des notes successives ;
on trouve
| ut | 9/8 | ré | 10/9 | mi | 16/15 | fa | 9/8 | sol | 10/9 | la | 9/8 | si | 16/15 | ut |
On voit qu’il existe trois sortes d’intervalles : le ton majeur (9/8), le ton mineur (10/9), et le demi-ton (16/15).
Ces trois intervalles se classent donc ainsi
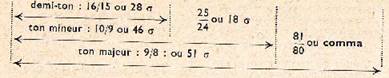
Transposer la gamme signifie changer de tonique, c’est-à-dire répéter la mélodie de la gamme à partir d’une nouvelle note. Le tableau précédent montre qu’un ton majeur correspond à 3 intervalles différents, et par conséquent, pour les 7 notes de la gamme, il faudrait 21 touches de clavier par gamme pour avoir à sa disposition tous les intervalles nécessaires en vue de la transposition : jouer d’un tel instrument serait inextricable.
L’écriture musicale deviendrait aussi pratiquement impossible : dièser une note (passer d’un demi-ton à un ton mineur ou à un ton majeur) signifierait multiplier sa fréquence par 25/24 ou par 25/24x81/80 ; bémoliser serait effectuer l’une ou l’autre opération en sens inverse. On verrait facilement qu’un ut dièse ne coïncide pas avec un ré bémol.
| ut | 25/24 ou 18 σ | ut dièse | 25.92/25 ou 15 σ | ré bémol | 25/24 ou 18 σ | ré |
.
C’est pour toutes ces raisons, à cause surtout des instruments à son fixe, que l’on a adopté la gamme de Bach.
w. Gamme tempérée
La gamme tempérée fut imposée par l’illustre musicien Jean-Sébastien Bach (1685-1750), après de nombreuses discussions auxquelles prirent part Rameau et d’Alembert. Tous les pianistes connaissent le « Clavecin bien tempéré » (1722-1744).
Les notes de cette gamme partagent l’intervalle d’octave en douze intervalles égaux appelés demi-tons tempérés.
L’intervalle d’octave étant I = 2, soit en savarts
1000 log 2 = 301,03 σ
ou, avec une approximation suffisante 300 σ, chaque demi-ton tempéré vaut 300/12 = 25 σ
Un demi-ton tempéré vaut 25 σ ; un ton vaut toujours 50 σ. La transposition est alors des plus faciles. En prenant la note ut pour tonique, la gamme diatonique représente une certaine mélodie dont les intervalles successifs sont
1 ton — 1 ton — 1/2 ton — 1 ton — 1 ton — 1 ton — 1/2 ton. Cette suite constitue la gamme diatonique.
Si la nouvelle tonique est le fa, il suffira d’élever d’une quinte, soit de 5 demi-tons, toutes les notes de la gamme, ce qui sera toujours possible puisque l’on dispose sur le clavier de toutes les notes de demi-ton en demi-ton.
On jouera alors
fa sol la si_bémol do ré mi fa.
Si l’on transpose en la
la si do_dièse ré mi fa_dièse sol_dièse la.
Les règles de l’harmonie indiquent quand il faut écrire do_dièse au lieu de ré_bémol, bien que ces deux notes soient identiques dans la gamme tempérée.
Les touches d’un clavier d’orgue ou de piano correspondent à chaque note des gammes successives. On remarque des touches blanches (fig. 267) entre lesquelles s’intercalent certaines touches noires. Les notes correspondant aux touches blanches donnent la gamme diatonique ordinaire, que l’on s’accorde à considérer comme le type d’une mélodie parfaite, en prenant le ut pour tonique (note de départ).
Les notes correspondant aux touches noires sont considérées comme des altérations des notes précédentes. Ce sont : ut_dièse (ut dièse : ut naturel augmenté d’un demi-ton) identique à ré_bémol (ré bémol : ré naturel diminué d’un demi-ton), et ainsi de suite. La succession de toutes les notes donne la gamme chromatique (succession ce demi-tons).
 Fig. 267
Fig. 267
Accords. — La musique utilise des accords tels que l’accord parfait majeur ut, mi, sol ; l’accord parfait mineur : ut, mi_bémol, sol ; l’accord dissonant : sol, si, ré, fa, ainsi qu’une foule d’autres, et cela dans des tons différents (avec des toniques différentes) ; l’harmonie est la science très précise et difficile de l’enchaînement des accords entre eux.
Registres.— Les divers instruments et les différentes voix humaines utilisent des ensembles de notes appelés leurs registres. L’orgue utilise tous les sons audibles depuis les plus graves (tuyau de 32 pieds) jusqu’aux plus aigus (tuyaux de quelques millimètres) ; le piano va de la-2 (27 vibrations) à la6 (3480 vibrations). La figure 268 représente les tessitures des voix humaines, c’est-à-dire l’intervalle des notes extrêmes les plus usitées dans chacun des registres indiqués ; exceptionnellement le soprano donne le sol5, et certaines basses russes le la-1
 Fig.268
Fig.268
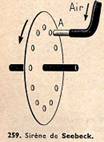 Fig.259
Fig.259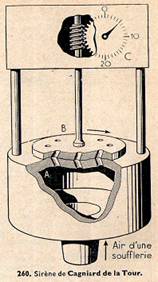 Fig.260
Fig.260